Καλωσήλθατε στην κεντρική σελίδα του Ε.Κ.Φ.Ε. Καστοριάς !
 |
«ΚΟΣΜΟΝ ΤΟΝΔΕ , ΤΟΝ ΑΥΤΟΝ ΑΠΑΝΤΩΝ, ΟΥΤΕ ΤΙΣ ΘΕΩΝ ΟΥΤΕ ΤΙΣ ΑΝΘΡΩΠΩΝ ΕΠΟΙΗΣΕΝ, ΑΛΛ΄ ΗΝ ΑΕΙ ΚΑΙ ΕΣΤΙΝ ΚΑΙ ΕΣΤΑΙ ΠΥΡ ΑΕΙΖΩΟΝ, ΑΠΤΟΜΕΝΟΝ ΜΕΤΡΑ ΚΑΙ ΑΠΟΣΒΕΝΝΥΜΕΝΟΝ ΜΕΤΡΑ» Ηράκλειτος |
|
ΣΥΝΘΕΣΗ ΤΑΛΑΝΤΩΣΕΩΝ
Σε ένα σώμα γίνεται σύνθεση ταλαντώσεων, όταν το ίδιο σώμα εξαναγκάζεται σε τουλάχιστον δύο ταλαντώσεις ταυτόχρονα. Η τελική κίνηση, που ονομάζεται σύνθετη ταλάντωση, είναι αρκετά περίπλοκη. Η διεύθυνση της τελικής ταλάντωσης, το πλάτος, η φάση και η θέση ισορροπίας, εξαρτώνται από τα αντίστοιχα των επιμέρους ταλαντώσεων.
Έστω χ1=Α1ημ(ω1t + φ1) και χ2=Α2ημ(ω2t+ φ2) οι εξισώσεις των συνιστωσών ταλαντώσεων. Γενικά οι ταλαντώσεις μπορεί να έχουν διαφορετικό πλάτος, συχνότητα, αρχική φάση, θέση ισορροπίας και διεύθυνση κίνησης.
Αν οι επιμέρους ταλαντώσεις γίνονται γύρω από την ίδια θέση ισορροπίας και στην ίδια διεύθυνση, τότε και η σύνθετη ταλάντωση θα έχει την ίδια Θ.Ι. και την ίδια διεύθυνση. Με τις δύο αυτές προϋποθέσεις ισχύει η σχέση χ=χ1+χ2 όπου χ η απομάκρυνση της σύνθετης ταλάντωσης και χ1 , χ2 οι απομακρύνσεις την ίδια χρονική στιγμή των συνιστωσών ταλαντώσεων.
|
Στην προσομοίωση δίπλα, με κόκκινο χρώμα είναι η 1η ταλάντωση, με μπλέ χρώμα είναι η 2η ταλάντωση και με μαύρο είναι η σύνθεσή τους. Οι ταλαντώσεις γίνονται γύρω απο την ίδια θέση ισορροπίας και στην ίδια διεύθυνση. Αφήστε την τιμή φ1=0, και δείτε το αποτέλεσμα της σύνθεσης για διάφορες τιμές της φ2, και στα πλάτη Α1,Α2. Αλλάξτε τις τιμές f1 και f2, διατηρώντας την ισότητα f1=f2 (κοινή συχνότητα). Παρατηρήστε οτι με την προϋπόθεση f1=f2, προκύπτει πάντα αρμονική ταλάντωση. Το πλάτος της σύνθεσης και η τιμή της αρχικής απομάκρυνσης (αρχική φάση ) καθορίζονται απο τις τιμές Α1,Α2 και φ2 . Με τα βέλη up και dn ( ανάμεσα στο "Έναρξη/Συνέχεια" και "Επανεκίνηση" ) μπορείτε να δείτε τις δυο ταλαντώσεις στο ίδιο διάγραμμα.
Δοκιμάστε την σύνθεση στην περίπτωση f1?f2. Παρατηρήστε οτι η σύνθεση είναι περιοδική, ΌΧΙ όμως αρμονική. Το διακρότημα θα εμφανισθεί όταν Α1=Α2 και f1?f2. Θέστε f1=1Hz , f2=0,9Hz και A1=A2=50. |
|
Περίπτωση 1η
- Κοινή θέση ισορροπίας
- Ίδια διεύθυνση ταλάντωσης
- ω1=ω2
Σε κάθε περίπτωση θα συμβολίζουμε με χ1=Α1ημ(ω1t ) και χ2=Α2ημ(ω2t+ φ) τις εξισώσεις των συνιστωσών ( αρχικών) ταλαντώσεων. Στην περίπτωση αυτή θεωρούμε t=0 τη στιγμή που η μία απο αυτές ( χ1) έχει απομάκρυνση μηδέν και θετική ταχύτητα (αρχική φάση της 1ης μηδέν).
Στην περίπτωση αυτή οι εξισώσεις ταλάντωσης είναι: χ1=Α1ημ(ωt) και χ2=Α2ημ(ωt+φ) (Θα συμβολίζουμε χ1 την ταλάντωση με μηδενική αρχική φάση.)
Αποδεικνύεται μαθηματικά οτι το αποτέλεσμα της σύνθεσης είναι χ= Α ημ(ωt+θ).
Η σύνθετη ταλάντωση έχει νέο πλάτος Α, ίδια γωνιακή συχνότητα ω και διαφορά φάση σε σχέση με την χ1 κατά θ.
Για να προσδιορισθεί η σύνθετη ταλάντωση πρέπει να βρεθεί το νέο πλάτος Α και διαφορά φάσης θ σε σχέση με την χ1.
Αποδεικνύεται οτι το πλάτος και η γωνία υπολογίζονται απο τις σχέσεις :
 |
 |
| Το νέο Πλάτος. | Η διαφορά φάσης σε σχέση με την χ1. |
Ειδικές Περιπτώσεις:
| α) φ=0 χ1=Α1ημ(ωt) και χ2=Α2ημ(ωt) | Α=Α1+Α2 και θ=0 | χ=(Α1+Α2)ημ(ωt) |
| β) φ=π χ1=Α1ημ(ωt) και χ2=Α2ημ(ωt+π) | Α1>Α2 ? Α=Α1-Α2 και θ=0 | χ1=(Α1-Α2)ημ(ωt) |
| Α1<Α2 ? Α=Α2-Α1 και θ=π | χ1=(Α2-Α1)ημ(ωt+π) | |
| Α1=Α2 ? Α=0 | χ1=0·ημ(ωt+θ)=0 |
Περίπτωση 2η
- Κοινή θέση ισορροπίας
- Ίδια διεύθυνση ταλάντωσης
- ω1?ω2
- Α1=Α2 =Α
- φ1=φ2=0
Στην περίπτωση αυτή οι εξισώσεις ταλάντωσης είναι: χ1=Αημ(ω1t) και χ2=Αημ(ω2t)
Η σύνθεση των αρμονικών ταλαντώσεων αυτών δίνει μια νέα ταλάντωση γύρω από την ίδια θέση ισορροπίας, στην ίδια διεύθυνση, μόνο που δεν είναι αρμονική. Η εξίσωση της ταλάντωσης είναι :
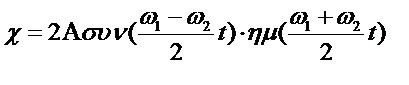
Ορίζουμε ως πλάτος Α' τον παράγοντα :
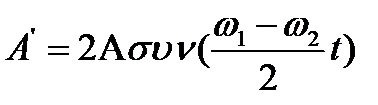
και έτσι η εξίσωση έχει την μορφή :
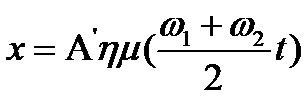
Η ταλάντωση που περιγράφεται από την παραπάνω εξίσωση ΔΕΝ είναι απλή αρμονική ταλάντωση γιατί το πλάτος Α' είναι συνάρτηση του χρόνου και μεταβάλλεται "αργά" όταν οι συχνότητες διαφέρουν ελάχιστα μεταξύ τους. Η ταλάντωση του σώματος σε αυτήν την περίπτωση ονομάζεται διακρότημα και ο χρόνος μεταξύ δύο διαδοχικών μηδενισμών (ή μεγίστων) του πλάτους ονομάζεται περίοδος του διακροτήματος.
Στο σχήμα 1 φαίνεται η σύνθεση των χ1=2ημ(5t) και χ2=2ημ(9t) Η σύνθεση είναι περιοδικά αλλά όχι αρμονική. Οι γωνιακές συχνότητες διαφέρουν αρκετά και έτσι δεν παρουσιάζεται η μορφή του διακροτήματος.
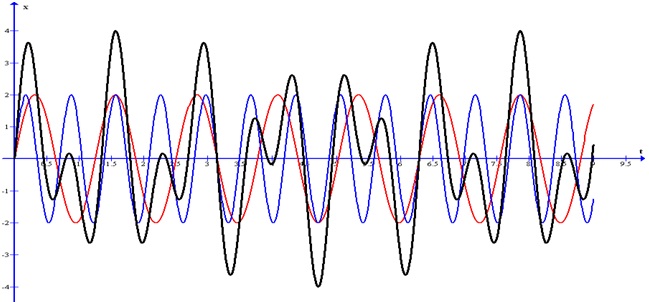 Σχήμα 1
Σχήμα 1
Στην ειδική περίπτωση που ω1?ω2, τότε εμφανίζεται κίνηση της οποίας η απομάκρυνση έχει γραφική παράσταση όπως στο σχήμα 2
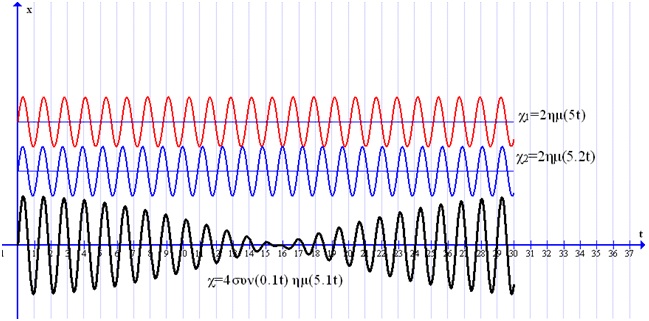 Σχήμα 2
Σχήμα 2
Παρατηρήστε στο σχήμα 2 ότι αφενός γίνονται ταλαντώσεις, αφετέρου το πλάτος των ταλαντώσεων αυξομειώνεται. Έτσι για την κίνηση αυτή ορίζεται η περίοδος της ταλάντωσης και η περίοδος αυξομείωσης του πλάτους. Η δεύτερη ονομάζεται περίοδος του διακροτήματος.
Προφανώς η περίοδος του διακροτήματος είναι μεγαλύτερη από την περίοδο ταλάντωσης.
Στην έκφραση
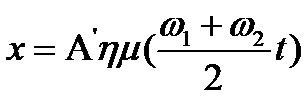 ο παράγοντας ημ (ω1+ω2)/2 , καθορίζει την συχνότητα (άρα και την περίοδο) της ταλάντωσης που είναι f=(f1+f2)/2. Δηλαδή f? f1? f2 αφού f1? f2.
ο παράγοντας ημ (ω1+ω2)/2 , καθορίζει την συχνότητα (άρα και την περίοδο) της ταλάντωσης που είναι f=(f1+f2)/2. Δηλαδή f? f1? f2 αφού f1? f2.
Η συχνότητα του διακροτήματος υπολογίζεται απο τη σχέση
fδ=|f1-f2| .
Παράδειγμα σύνθεσης διακροτήματος.
Έστω ταλαντώσεις με χ1=10ημ(101πt) και χ2=10Αημ(99πt)
Η συχνότητα της πρώτης είναι f1=50,5Hz και της δεύτερης f2=49,5Hz.
Η σύνθεση έχει εξίσωση χ=20συν(πt)ημ(100πt)
Στο σχήμα φαίνονται οι γραφικές παραστάσεις των τριών ταλαντώσεων.
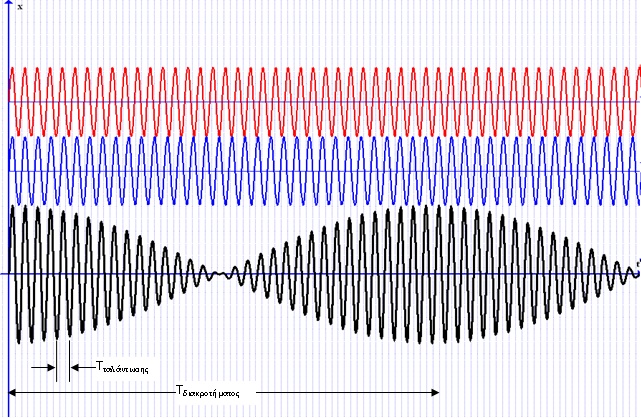
Η συχνότητα της ταλάντωσης είναι f=50 Hz ( μέση τιμή των 50,5Ηz και 49,5Ηz ) ενώ η συχνότητα του διακροτήματος είναι fδ= 1 Hz.
ΑΣΚΗΣΕΙΣ
Ασκ 1. Ένα σώμα εκτελεί ταυτόχρονα δύο αρμονικές ταλαντώσεις ίδιας διεύθυνσης , ίδιας Θ.Ι. με εξισώσεις : χ1 = 5ημ20t και χ1 = 5ημ(20t+φ) στο S.I. . Να γράψετε την εξίσωση της σύνθετης ταλάντωσης στις περιπτώσεις α] φ=0 β] φ=π/3 rad γ] φ=π/2 rad δ] φ=π rad
Ασκ 2. Ένα σώμα εκτελεί ταυτόχρονα δύο αρμονικές ταλαντώσεις ίδιας διεύθυνσης , ίδιας Θ.Ι. με εξισώσεις : χ1 = 5ημ20t και χ1 = 5ημ(20t+π/2) στο S.I.
- Να γράψετε την εξίσωση της απομάκρυνσης και ταχύτητας της σύνθετης ταλάντωσης.
- Να βρεθεί ποια χρονική στιγμή είναι η απομάκρυνση της σύνθετης ταλάντωσης χ=5 m , 1η φορά.
- Ποια είναι η ενέργεια της ταλάντωσης, αν η μάζα του σώματος είναι m=2Kgr;
Ασκ 3. Ένα σώμα εκτελεί ταυτόχρονα δύο απλές αρμονικές ταλαντώσεις που εξελίσσονται πάνω στην ίδια ευθεία και γύρω από την ίδια θέση ισορροπίας. Οι εξισώσεις των απομακρύνσεων για τις δύο ταλαντώσεις είναι αντίστοιχα:
χ1=0,4ημ(πt/3) και χ2=0,4?3ημ(πt/3+π/2)
- Να γραφεί η εξίσωση της απομάκρυνσης για τη συνισταμένη ταλάντωση.
- Να προσδιοριστεί η πρώτη φορά κατά την οποία το σώμα βρίσκεται στη θέση χ = + A .
Ασκ 4. Δύο απλές αρμονικές ταλαντώσεις εξελίσσονται πάνω στην ίδια ευθεία και γύρω από την ίδια θέση ισορροπίας. Οι εξισώσεις των απομακρύνσεων για τις δύο ταλαντώσεις είναι αντίστοιχα: χ1 = 5ημ2πt και χ2 = 5 ημ(2πt + π/2) (χ1,χ2 σε cm). Ζητείται:
- Να υπολογισθεί η εξίσωση της απομάκρυνσης για τη συνισταμένη ταλάντωση.
- Να υπολογισθεί η επιτάχυνση τη χρονική στιγμή t = 0.25 sec. Δίνεται π2 =10.
Ασκ 5. Ένα σώμα εκτελεί ταυτόχρονα δύο απλές αρμονικές ταλαντώσεις που εξελίσσονται πάνω στην ίδια ευθεία και γύρω από την ίδια θέση ισορροπίας. Οι εξισώσεις των απομακρύνσεων για τις δύο ταλαντώσεις είναι αντίστοιχα:
χ1=20ημ(4πt+π/3) και· χ2=204?3ημ(4πt-π/6)
- Να γραφεί η εξίσωση της απομάκρυνσης για τη συνισταμένη ταλάντωση,
- Να προσδιοριστεί η χρονική στιγμή κατά την οποία το σώμα βρίσκεται στη θέση όπου για πρώτη φορά μηδενίζεται η ταχύτητα του.
Ασκ 6. Το πλάτος διακροτήματος δίνεται από τη σχέση Α = 10συν(t). Το δημιουργούν δύο απλές αρμονικές ταλαντώσεις που εξελίσσονται ταυτόχρονα προς την ίδια διεύθυνση, γύρω από την ίδια θέση ισορροπίας με το ίδιο πλάτος και χωρίς αρχική φάση. Οι συχνότητες είναι f1=30/π Hz και f2. Να υπολογίσετε την εξίσωση του διακροτήματος και τις εξισώσεις των συνιστωσών ταλαντώσεων.
Ασκ 7. Η εξίσωση x=A?ημ(ω?t+φ) είναι το αποτέλεσμα της σύνθεσης δύο άλλων ταλαντώσεων xΑ και xΒ για τις οποίες παρέχονται οι εξής πληροφορίες:
- Οι xΑ και xΒ εξελίσσονται στην ίδια ευθεία με την ίδια συχνότητα f = 5ΗΖ .
- Τη χρονική στιγμή t=0 παρουσιάζουν ίσες απομακρύνσεις ενώ η ταχύτητα της xΒ είναι τριπλάσια της xΑ και αντίθετης φοράς.
- Τη χρονική στιγμή t=1/30sec η ταχύτητα της xΑ λαμβάνει τη μέγιστη τιμή της π m/sec.
Να προσδιορίσετε την εξίσωση της συνισταμένης κίνησης και να υπολογίσετε την απομάκρυνση της συνισταμένης κίνησης την στιγμή που η xΑ παρουσιάζει μηδενική απομάκρυνση ενώ η xΒ έχει θετική απομάκρυνση.